Accueil

Préambule

Objectifs

Verilog a une syntaxe proche de celle du C. Les types de données sont eux aussi proches de ceux du C, avec des extensions spécifiques au matériel. 

L'objectif de ce chapitre est de vous présenter les types définis par Verilog, ainsi que les expressions utilisables. A l'issue de ce chapitre, vous serez en mesure de choisir le meilleur type pour l'objet que vous voulez modéliser.

Plan du chapitre

Remarque importante

Ce chapitre, comme tous les chapitres sur la syntaxe des langages, est un peu indigeste. Il vaut mieux le voir comme une référence, une page à laquelle vous pourrez vous rapporter tout au long du cours, ou en cas de problème. Par contre, il est conseillé de l'avoir lue au moins une fois, pour garder en tête où se trouvent les pièges éventuels.

Back to Top

Conventions lexicales

Les conventions lexicales de Verilog sont les mêmes que celles utilisées en C. Un code Verilog est composé d'une suite d'éléments :

Verilog est sensible à la casse : tous les mots clefs doivent être en minuscules.

Espaces

Les espaces peuvent être au choix un espace normal (\b), une tabulation (\t) ou un retour à la ligne (\n).
Les espaces sont ignorés, sauf quand ils séparent des éléments, ou à l'intérieur des chaînes de caractères.

Commentaires

Des commentaires doivent être inclus dans le code, pour augmenter la lisibilité et la documentation.
Il en existe deux styles, comme en C :

Les commentaires à lignes multiples ne peuvent pas être imbriqués.
Un commentaire ne peut pas couper un identificateur ou un mot-clef.

Il est impératif de documenter vos codes, à l'école comme en entreprise.

Underscore

Les underscore "_" peuvent apparaître dans les identificateurs ou dans les nombres (sauf en premier caractère). Ils servent surtout à augmenter la lisibilité du code.

Identificateurs

Ce sont les noms de variables, de signaux, de fonctions, ...

Attention : majuscules et minuscules sont différenciées



Back to Top

Valeurs logiques

Verilog utilise un système à 4 valeurs :

Voici quelques tables de vérité multi-valuées :

Tables de vérités multivaluées

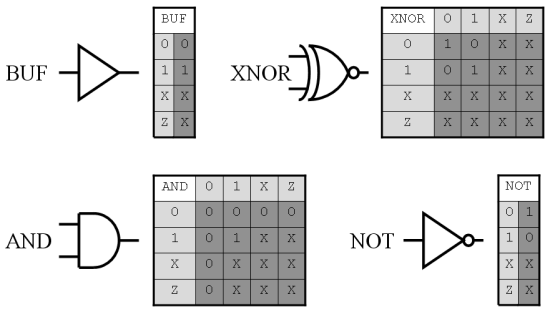
Tables de vérité multi-valuées

Des forces peuvent éventuellement être appliquées aux valeurs logiques pour résoudre d'éventuels conflits en cas de pilotes (drivers) multiples. Par ordre décroissant :

Si deux signaux différents sont appliqués à un signal, celui de plus grande force prévaut, et la force du résultat est alors la plus grande des deux.
Si deux signaux différents de même force sont appliqués à un signal, le résultat est inconnu (x).

Les forces de signaux sont surtout utilisées pour modéliser les transistors MOS et autres dispositifs de très bas niveau.

Back to Top

Types de données

Noeuds

Les noeuds représentent les connexions entre des éléments physiques. Ils sont principalement utilisée en description structurelle (instanciation de portes ou de modules).
Comme dans le monde réel, leur valeur leur est assignée continuement, autrement dit ils n'ont pas de capacité de mémorisation.
Par défaut, la valeur d'un noeud est Z (sauf pour les trireg, dont la valeur par défaut est x)

Le mot clef pour déclarer un noeud est généralement wire.

A moins de le préciser, un wire est sur un seul bit. On peut cependant déclarer un ensemble de noeuds, un bus.
Exemple :

wire a;                 // déclare un noeud, a, sur 1 bit
wire b, c, d;           // déclare trois noeuds, b, c, et d, sur 1 bit chacun
wire [7:0] bus1;        // déclare un bus de 8 noeuds bus1.
wire [2:13] bus2, bus3; // déclare deux bus de 12 bits chacun, bus2 et bus3.

Lors de la déclaration d'un bus, le bit de poids fort est toujours à gauche, celui de poids faible à droite. Dans l'exemple ci-dessus, le poids fort de bus2 est numéroté 2, celui de bus1 est numéroté 7.
On peut accéder à un élément particulier d'un bus ou à une partie de bus.
Lors de l'accès à une partie de bus, l'ordre des indices doit respecter l'ordre de déclaration.

... = bus1[3] ...   // 4ème bit de bus1
... = bus1[6:2] ... // bus formé des 5 bits de bus1, dans l'ordre 6, 5, 4, 3 et 2. ... bus2[3:6]... // CORRECT
... = bus2[6:3]...  // INCORRECT
... = bus1[2:4]...  // INCORRECT
... = bus1[4:2]...  // CORRECT

Il existe d'autres types de noeuds :

tri
même chose que wire. La convention veut que wire est utilisé dans le cas d'un pilote simple, tri dans le cas de pilotes multiples.
wand/triand
ce sont des ET câblés. L'affectation de signaux différent à ces noeuds se résoudra par un ET des deux signaux.
wor/trior
même chose,en OU câblés.
supply0, supply1
déclaration d'un noeud d'alimentation, de force supply. 
tri0, tri1, trireg, ...
peu usités... représentent des pull-down, pull-up, ou un réseau capacitif. On se rapportera à la norme Verilog pour plus de détails.

Remarque : on utilise dans 99% des cas des wire.

Les wire sont par défaut non signés. Si on les veut signés, on leur adjoint le mot-clef signed (voir ci-dessous).

Variables

Les variables se distinguent des noeuds par le fait qu'elles ont des capacités de mémorisation.

On ne leur assigne pas de valeur en continu, mais seulement à des moments précis. Elles gardent alors cette valeur jusqu'à la prochaine affectation. Elles sont donc utilisées pour des descriptions comportementales seulement.

Les variables ont deux rôles :

Attention : la version de Verilog 1995 appelle les variables "registers". Ce terme a été retiré de la norme, et remplacé par le terme "variable", car il entrainait trop de confusions entre "registre au sens Verilog" (un objet mémorisant) et "registre au sens matériel" (bascule D) : une variable peut modéliser une bascule D, mais peu aussi modéliser un fil ou une fonction purement combinatoire.

Une variable est généralement déclarée par reg. 

Par défaut, un reg est sur 1 bit. Comme pour les wire, on peut en faire des bus.
Les reg sont par défaut non signés. Si on les veut signés, on leur adjoint le mot-clef signed. Ils sont alors représentés en complément à 2. 

Exemple :

reg signed [3:0] a;
reg signed [7:0] b;
reg [3:0] c;
reg [7:0] d;

initial
begin
  a = -1;
  b = a;
  $display("a=%b, b=%b", a, b);
end

initial
begin
  c = -1;
  d = c;
  $display("c=%b, d=%b", c, d);
end

Exercice

Les autres variables :

integer
similaires aux reg, mais signés. Sa taille est la taille de mots de la machine hôte, généralement 32bits.
ils sont utilisés pour compter, alors que les reg sont utilisés pour les signaux sur 1 bit, et généralement comme variables locales.
real
définissent des nombres réels signés, représentés selon la norme IEEE Std 754-1985, un standard sur la représentation des flottants en double précision.
peuvent être utilisés en notation
  • décimale : 1.2, 0.142, -478.34
  • scientifique : 4e10, -4.30e-3
les conversion réels vers entiers se fait vers l'entier le plus proche avec la convention :
  • 0.5 devient 1
  • -0.5 devient -1
leur valeur par défaut est 0.
time
pour stocker des temps de simulation
implémentation spécifique à chaque plate-forme, mais au minimum 64 bits, et leur bit de poids faible est toujours à 0.
realtime
pour stocker des temps de simulation, mais sous forme flottante
implémentation spécifique à chaque plate-forme, mais au minimum 64 bits.
Paramètres

Les paramètres sont un type particulier de variables : ils définissent des constantes. Ces constantes permettent de construire des blocs génériques. Par exemple, au lieu de coder trois additionneurs différents (un sur 8 bits, un sur 16, un sur 32), on n'en codera qu'un seul. Les bus internes seront définis en fonction d'un paramètre, qui pourra être modifié au moment de la compilation pour valoir 8, 16 ou 24.

C'est une très mauvaise habitude de coder un nombre en dur dans un code quel qu'il soit. Il vaut bien mieux définir un paramètre (ou utiliser les #define de C), et utiliser ce paramètre en lieu et place du nombre. Les paramètres de Verilog permettent d'avoir des #define du C un peu plus souples (ayant une portée locale seulement).

Le type des paramètres peut être explicite, implicite ou à mi-chemin entre les deux (partiellement implicite). Les règles suivantes permettent de  clarifier les choses :

L'utilisation des paramètres se fait comme-ceci :

Paramètres de spécification temporelle (specparam)
Pour spécifier des temps de propagation, setup, hold, etc., on utilise des paramètres d'un type spécial : specparam. Ils diffèrent des paramètres normaux sur les points suivants :
Les specparams sont déclarés soit dans un module, éventuellement dans un bloc specify.

Exemple :

module RAM;
  specify
    specparam tRise_clk_q = 150, tFall_clk_q = 200.23;
    specparam tRise_control = 40.0, tFall_control = 50;
  endspecify

...

endmodule
Chaînes de caractères

Les chaînes de caractères sont définies comme des bus (vecteurs) de reg. Chaque caractère étant codé sur 8 bits, une chaîne sera donc stockée sur un multiple de 8 regs.
Lors de l'affectation d'une chaîne,

Exemple :

module test_chaines;
  reg [8*9:1] ma_chaine;
  initial begin
    ma_chaine = "coucou";
    $display("%s est memorise comme %h", ma_chaine, ma_chaine);

    ma_chaine = {ma_chaine, "!!!"};
    $display("%s est memorise comme %h", ma_chaine, ma_chaine);

    ma_chaine = "coucou tres long";
    $display("%s est memorise comme %h", ma_chaine, ma_chaine);
  end
endmodule

qui produit la sortie suivante :

coucou est memorise comme 000000636f75636f75
coucou!!! est memorise comme 636f75636f75212121
tres long est memorise comme 74726573206c6f6e67

Back to Top

Codage des nombres entiers

En Verilog, les nombres entiers peuvent :

La représentation générique d'un entier est [signe] [taille ' [s] base] <valeur>.


Chaque nombre porte, en plus de sa valeur, une information indiquant s'il est signé ou non : comment il doit être interpété, en cas d'expansion notamment (extension de signe ou non). Les règles suivantes déterminent si un nombre est signé ou non :

Si taille est plus grande que nécessaire pour représenter valeur, alors Verilog comble les bits de gauche ainsi :


Exemple :

4'd5   : nombre non signé sur 4 bits, valant 5
-4'd5  : nombre non signé sur 4 bits, valant 11 (-5 modulo 16)
4'sd5  : nombre signé sur 4 bits valant 5
-4'sd5 : nombre signé sur 4 bits valant -5
-5     : nombre signé sur au moins 32 bits valant -5
5      : nombre signé sur au moins 32 bits valant +5

Astuce : un petit algorithme pour bien interpréter les nombres :

  1. on commence avec n = [signe]<valeur>. 
  2. si on n'a pas de taille,  alors c'est fini, on a notre résultat. De plus, le résultat est signé.
  3. si on a une taille, alors on tronque / expanse n au bon nombre de bits, en faisant une extension de signe uniquement si 's' est spécifié.
  4. on a notre résultat. De plus, si on a 's' alors le résultat est signé, sinon non.


Exercice :

  1. Que va afficher le code suivant ?
module codage_nombres;

initial
  begin
    $display("%d", -6'd1);
    $display("%d", -6'sd1);
    $display("%d", -15);
    $display("%d", 4'shF);
    $display("%d", -4'shF);
    $display("%d", 4'hF);
    $display("%d", -4'hF);
    $display("%d", -'hF);
    $display("%d", 'hF);
  end

endmodule


Exercice :

  1. Que va afficher le code suivant ?
module codage_nombres_reloaded;

initial
  begin
    // En binaire
    $display("%b", -12);
    $display("%b", -'d12);

    // Idem, mais en décimal
    $display("%d", -12);
    $display("%d", -'d12);

    // Juste pour être sûr (% : modulo)
    $display("%d", -12 % 3);
    $display("%d", -'d12 % 3);
  end

endmodule



Back to Top

Tableaux

Comme dans tous les langages (ou presque ?), il possible de déclarer des tableaux multi-dimensionnels. On peut déclarer des tableaux de noeuds (wire) ou de variables (reg, integer, ...).
Les éléments du tableaux peuvent être

La déclaration de tableaux se fait en spécifiant l'étendue des dimensions entre crochets après le nom de l'instance (une déclaration d'étendue avant le nom sert à déclarer un bus).
Exemple :

Attention : ne pas confondre un tableau de scalaires (reg xxx [7:0]) et un bus (reg [7:0] xxx). Un bus peut être affecté en une seule instruction, tandis qu'un tableau ne peut pas : on ne peut accédér qu'à un seul élement du tableau à la fois.

Lors d'un accès à un tableau multidimensionnel, on doit spécifier un index pour toutes les dimensions : en d'autres termes, on ne peut pas extraire une ligne (ni une colonne) d'une matrice.

Les tableaux sont utiles pour modéliser les mémoires : une mémoire est un tableau de mots (un mot est un vecteur de bits).
On a le droit, lors de l'accès à un tableau, de spécifier l'index par un reg (ou tout autre type entier). Mais attention, cette construction n'est souvent pas synthétisable.

Exemple :

reg [7:0] tab [1023:0];
reg index;

initial
  begin
    index = 0;
    tab[index] = 8'b1100_0101;
  end

Back to Top

Expressions et opérateurs

Lors d'une affectation continue, on affecte à un noeud une expression, constante ou non (comme dans l'exemple ci-dessus). Les expressions peuvent être utilisées non seulement dans les affectation continues, mais aussi dans les autres types d'affectation que nous verrons plus tard. C'est l'occasion de les étudier !

Une expression combine des opérateurs et des opérandes. Une opérateur (&, |, +, ...) peut agir sur une, deux ou trois opérandes.
Les opérandes peuvent être :

Les opérateurs peuvent être :

Tous les opérateurs ne sont pas applicables à certains types. Pour les réels, les opérateurs suivants ne peuvent pas être utilisés :

Le résultat d'une opération logique ou relationelle sur des réels est un bit.

 
Priorité des opérateurs

La priorité des opérateurs suit la convention du C.
Voici un récapitulatif des priorités des opérateurs. Des opérateurs sur la même ligne ont la même priorité : les parenthèses sont alors nécessaires.
De toutes façons, les parenthèses sont une bonne habitude, ne serait-ce que pour rendre le code plus lisible !

+ - ! ~ (unaires) plus prioritaire
 ** 
 * / % 
+ - (binaires)
 << >> <<< >>> 
 < <= > >= 
 == != === !== 
 & ~& 
 ^ ^~ ~^ 
 | ~| 
 && 
 || 
?: (conditional operator)  moins prioritaire 

Priorité des opérateurs

 
Opérateurs arithmétiques

Les opérateurs arithmétiques sont les suivants :

  Opérateur   Commentaires
 a + b  somme
 a - b  différence
 a * b  produit
 a / b  division; la division entière tronque vers zéro.
 a % b  modulo; du signe de a
 a ** b  puissance (a puissance b)
 +a  prioritaire sur les autres (opérateur unaire)
 -a  prioritaire sur les autres (opérateur unaire)

On fera attention au signe des opérandes (voir ici pour plus de détails).

On fera attention aussi au nombre de bits de l'expression. Pour cela on se rapportera à la section sur la longueur en bit des expressions.

Exemples :

wire [15:0] sommeA;
wire [16:0] sommeB;

wire [15:0] a, b;

assign sommeA = a + b; // l'addition se fait sur 16 bits.
assign sommeB = a + b; // l'addition se fait sur 17 bits.
 
Opérateurs relationnels

Ce sont les opérateurs de comparaison. Le résultat d'une comparaison est


  Opérateur   Commentaires
 a < b  a strictement plus petit que b
 a > b    a strictement plus grand que b  
 a <= b  a plus petit ou égal à b
 a >= b  a plus grand ou égal à b

Si les opérandes ne sont pas de la même taille et qu'au moins l'un des deux est non signé, le plus petit est complémenté à gauche avec des 0, et la comparaison s'effectue sur des nombres non signés.
Si les deux opérandes sont signées, la relation est interprétée normalement (comme une comparaison sur des nombres signés...)
Si l'une des deux opérandes est un réel, l'autre opérande est automatiquement convertie en réel.

 
Opérateurs d'égalité

Le résultat est 0, 1 ou x.
Les opérandes sont comparées bit à bits, en complémentant le plus petit avec des 0 si nécessaire.

Pour == et !== (égalité et non-égalité), le résultat vaut x si l'une des deux opérande contient des x ou z.
Pour === et !=== (égalite et non-égalite), les x et z sont aussi comparés.

 
Opérateurs logiques

Les opérateurs logiques ont comme résultat 0, 1 ou x.

Opérateur Commentaires
 a && b  a ET b
 a || b  a OU b
 !a  NON a

Ces opérateurs travaillent sur des bits, sauf l'opérateur unaire ! qui peut accepter un type vecteur.
Le résultat de !a vaut :

 
Opérateurs binaires

Les opérateurs binaires opèrent sur des bits ou des vecteurs (bus), bit-à-bit.

Opérateur Commentaires
 &  ET
 |  OU
 ^  XOR
 ~^ ^~  XNOR
 ~  NOT (bit à bit)

Si les deux opérandes n'ont pas la même taille, le plus petit est complémenté à gauche avec des 0.

 
Opérateurs de réduction

Ce sont des opérateurs unaires (sur une seule opérande), opérant sur des vecteurs. Ils opèrent en fait sur les bits du vecteur passé en argument, en appliquant la fonction demandée à l'intégralité des bits du vecteur.
Le résultat est 0, 1 ou x.

Les opérations de base sont le ET, le OU et le XOR (&, |, ^).
Chaque opération dispose de sa version complémentée : c'est le résultat de l'opération qui est complémenté, pas les bits du vecteur.

Exemples :

 Opérande   &   ~&   |   ~|   ^   ~^ 
 4'b0000  0 1 0 1 0 1
 4'b1111  1 0 1 0 0 1
 4'b0110  0 1 1 0 0 1
 4'b0100  0 1 1 0 1 0

Si le vecteur contient un x ou un z, le résultat est x.

 
Opérateurs de décalage

Ces opérateurs opèrent des décalages (à droite ou à gauche) sur les bits de l'opérande de gauche.
Le sens du décalage est donné par l'opérateur.
Le nombre de position décalées est donné par l'opérande de droite (qui est considérée comme non signée).

  Opérateur   Commentaires
 >>   décalage vers la droite, les bits entrants sont des 0
 <<   décalage vers la gauche, les bits entrants sont des 0
 <<<   décalage vers la gauche, les bits entrants sont des 0
 >>> 

 décalage vers la droite. Le bit entrant est

  • un 0 si l'opérande est non signée
  • le MSB (signe) de l'opérande si l'opérande est signée

Attention à l'opérateur >>>. Le bit entrant dépend du type de l'opérande:

 
Opérateur conditionnel

C'est l'équivalent du if then else, sous forme d'équation. Sa syntaxe est la suivante : expr1 ? expr2 : expr3

L'opérateur conditionnel est très utilisé pour modéliser les sorties de portes 3-états :

wire [7:0] sortie, sortie_unbuf;
wire enable;

assign sortie = enable ? sortie_unbuf : 8'bzzzzzzzz;
 
Opérateur de concaténation

Cet opérateur permet de créer des bus à partir de bits ou de bus plus petits.
Exemple :

On peut aussi répliquer une expression.
Exemple :

Une concaténation peut être la cible d'une affectation :

wire [7:0] a, b;
wire cin, cout;
wire [7:0] somme;

assign {cout, somme} = a + b + cin;
 
Opérateurs d'événement

Ils seront étudiés plus tard !

Back to Top

Calcul des expressions : taille et type

Avant d'évaluer une expression, il est primordial de savoir sur combien de bits ça doit se faire.
Par exemple, lors de l'addition de deux bus de 8 bits, il est important de savoir si la somme est effectuée sur 8 bits ou sur 9 (permettant de détecter une retenue sortante).

Le calcul du nombre de bits s'effectue en deux temps : la taille intrinsèque d'une expression, puis un éventuel ajustement dans le cas d'une affectation.

Première étape : taille intrinsèque des expressions

La taille intrinsèque d'une expression est déterminée par la table suivante, das laquelle :

Expression   Taille (en bits) de l'expression  
 nombre constant sans taille  la même que celle d'un integer
 nombre constant de taille fixée  la taille du nombre
 x op y, avec op étant + - * / % & | ^ ^~ ou ~^  max(L(x), L(y)) 
 op x, avec op étant + - ou ~  L(x)
 x op y, avec op étant === !== == != && || > >= < ou <=  1 bit (après avoir éventuellement étendu la plus petite des opérandes)
 op x, avec op étant & ~& | ~| ^ ~^ ^~ ou !  1 bit
 x op y, avec op étant >> << ** >>> ou <<<  L(x)
  x ? y : z   max(L(y), L(z))
 {x, ..., y}  L(x) + ... + L(y) 
 {x{y, ..., z}}  x*(L(y) + ... + L(z)) 

Deuxième étape : ajustement éventuel

On appelle LHS le membre de gauche d'une affectation, RHS le membre de droite. On distingue trois cas :
Exercice :
  1. Que va afficher le code suivant ?
module add;

   reg [3:0]        a1, b1;
   reg [7:0]        answer1;
  
   reg signed [3:0] a2, b2;
   reg signed [7:0] answer2;
  
   reg [3:0]        a3, b3;
   reg [3:0]        answer3;

   initial begin
      a1  = 4'b1100;
      b1  = 4'b0100;
      a2  = a1;
      b2  = b1;
     
      a3  = 4'b0110;
      b3  = 4'b0110;
     
      // En non signé
      answer1 = a1 + b1;
      $display("a1 + b1 = %b", answer1);
      $display("a1 + b1 = %d", answer1);
      $display("a1 + b1 = %d", a1 + b1);

      // En signé
      answer2 = a2 + b2;
      $display("a2 + b2 = %b", answer2);
      $display("a2 + b2 = %d", answer2);
      $display("a2 + b2 = %d", a2 + b2);

      // Sur un même nombre de bits
      answer3 = a3 + b3;
      $display("a3 + b3 = %b", answer3);
      $display("a3 + b3 = %d", answer3);
      $display("a3 + b3 = %d", a3 + b3);

   end
  
endmodule


Attention : malgré tout, lors de l'évaluation d'une expression, les résultats intermédiaires peuvent perdre des bits.
Exemple :

wire [15:0] a, b, answer; // noeuds sur 16-bit
assign answer = (a + b) >> 1; // ne fonctionne pas correctement !

Dans l'exemple ci-dessus, on voudrait que la somme soit calculée sur 16 bits, avec éventuellement une retenu sortante, puis décalée de 1 bit vers la droite en faisant entrer l'éventuelle retenue.
Ce code ne fonctionne pas correctement : Expliquez pourquoi !!!

Une solution à ce problème serait de forcer le résultat intermédiaire à avoir une taille d'au moins 17 bits, ce qui peut se faire en ajoutant 0 (un entier, qui sera donc au moins sur 32 bits) :

wire [15:0] a, b, answer; // noeuds sur 16-bit
assign answer = (a + b + 0) >> 1; // fonctionne correctement
 
Exercices :
module bitlength();
  reg [3:0] a,b,c;
  reg [4:0] d;

  initial begin
    a = 9;
    b = 8;
    c = 1;
    $display("answer = %b", c ? (a&b) : d);
  end
endmodule

Signe d'une expression

En dehors de la taille d'une expression, il est important de savoir si elle sera signée ou non. Pour cela, les règles sont simples :

Récapitulation

On rassemble le tout ! Les expressions sont calculées ainsi :
  1. on calcule la taille du résultat (la taille de l'expression)  comme on l'a vu plus haut
  2. on calcul le type du résultat (s'il est signé ou non)
  3. on propage ce type et cette taille à toutes les opérandes là où ça a un sens
  4. on effectue les opérations...

Exercice :
  1. Que va afficher le code suivant ?
module piege();
  reg [3:0]  a;
  reg [5:0]  b;
  reg [15:0] c;

  initial begin
    a = 4'hF;
    b = 6'hA;
    $display("a*b=%h", a*b);

    c = {a**b};
    $display("a**b=%h", c);

    c = a**b;
    $display("c=%h", c);
  end
endmodule


  1. même question avec le code ci-dessous...
module LRM_arithmetic;
  integer    IA, IB;
  reg [15:0] RA, RB;

  initial
    begin
      IA = -4'd12;
      RA = IA / 3;
      RB = -4'd12;
      IB = RB / 3;
 
      $display(" hex default");
      $display("IA = -4'd12 = %h = %d", IA, IA);
      $display("RA = IA / 3 = %h = %d", RA, RA);
      $display("RB = -4'd12 = %h = %d", RB, RB);
      $display("IB = RB / 3 = %h = %d", IB, IB);

    end
endmodule

Back to Top

Directives de compilation

Verilog, comme C, accepte des directives de compilation (les équivalents des #define et #include...). Ces directives de compilation ont la forme suivante : `define et `include (le premier caractère est celui obtenu sur un clavier de PC par AltGr et 7).

Inclusion de fichiers

C'est l'équivalent du include de C : `include "nom_du_fichier".

Attention : si le nom du fichier spécifie un chemin relatif, alors c'est par rapport au répertoire d'où la simulation est lancée ! C'était le cas dans les anciens compilateurs C, mais ce comportement a été modifié depuis. Il est resté en Verilog, les gens s'occupant de la norme ayant eu peur de casser la sémantique des design existants.

Pour remédier à ce défaut, chaque outils propose des flags de compilation tels que INCDIR, permettant de spécifier les répertoires où l'outil doit chercher les fichiers inclus.

Définitions

Il est possible, comme en C avec les #define, de créer des macros textes à l'aide des directives `define et `undef. Mais contrairement au C, ces définitions ont un scope global : dès qu'elles sont rencontrées par le simulateur / synthétiseur, elles sont valables pour tous les fichiers lus après. Pour éviter des warning de re-définition de macros, il suffit d'utiliser des gardes, comme en C :

Exemple :
// incl.vh
`ifndef _incl_vh_
`define _incl_vh_

// On inclut tout ce qu'on veut
`define DEPTH 4
`define WIDTH (1 << `DEPTH)

`endif //_incl_vh_

Attention de ne pas abuser de ce mécanisme !  Certains objets (fonctions, tâches) ont besoin d'être ré-instanciés, par exemple les fonctions et tâches qui ont un scope local !..

Compilation conditionnelles

C'est comme en C :  `ifdef, `ifndef, `else, `elsif, `endif
Ces directives sont souvent utilisées pour séparer  code synthétisable et code non synthétisable : un attribut assez répandu étant synthesis, on peut écrire le code suivant :
....
`ifndef synthesis 
  $display("Je ne serai pas synthetisé !");
`endif

// Construction équivalente (mais moins élégante)
// pragma translate off
  $display("Je ne serai pas synthetisé !");
// pragma translate on

Types par défaut

Par défaut, un objet non déclaré est de type wire (net sur 1 bit). Il est possible de changer ce comportement en utilisant la directive `default_nettype <type>. 

Exemple : `default_nettype none oblige à déclarer explicitement tous les nets !

Ménage...

La directive `resetall permet de remettre à zéro toutes les directives de compilation précédentes (définitions, types par défaut etc...). On l'utilise typiquement en début de chaque fichier, suivi de toutes les définitions qu'on souhaite appliquer à ce fichier.


Back to Top

En résumé

On a vu

Il y a deux types principaux d'objets :

Tout type peut être signé ou non signé.

On peut déclarer des vecteurs (bus) et des tableaux multidimensionnels :

Les constructions à base de tableaux sont rarement correctement synthétisables.

La représentation des nombres entiers est parfois pénible si on oublie ce qu'on manipule.
Il vaut mieux parfois travailler sur des reg non signés, et faire attention lors des extensions de signe.

Les expressions utilisables sont celles du C, en faisant attention à la taille du résultat !

Prochain chapitre

Le prochain chapitre est moins "catalogue" : il vous présente les éléments structurels de Verilog, comment écrire et instancier des modules, comment les relier.

Back to Top