Ces exercices seront fait en Verilog, mais leurs principes restent les mêmes pour VHDL ou SystemC...

Exercice 1

On considère un compteur synchrone très simple :

• L’horloge H est générée par un processus à une fréquence de 50 MHz (soit une période de 20 ns).
• Les bascules D qui constituent le registre sont gérées par un deuxième processus. Le registre échantillonne sur front montant de l’horloge H. Son entrée est le signal D, sa sortie le signal Q.
• Enfin, un troisième processus assure la partie opérative proprement dite. Il calcule la valeur du signal D en fonction de la valeur du signal Q : D = Q + 1.

 

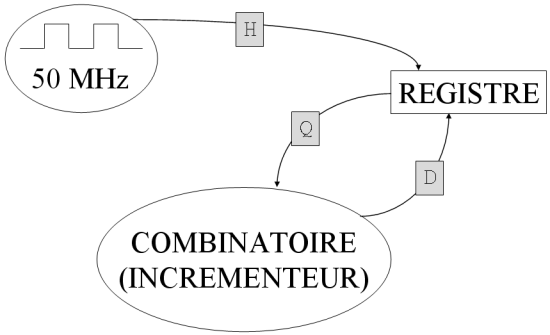
Schéma du compteur

Une description Verilog possible de ces trois processus est donnée dans la figure ci-dessous :

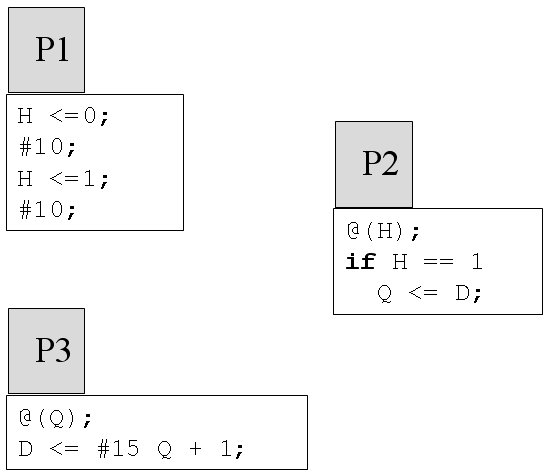
Description Verilog des trois processus

La notation @(signal) signifie que le processus en question est stoppé jusqu'à un événement sur signal (un changement d'état).
La notation #10; est un point d'arrêt sans liste de sensibilité. Le processus est stoppé, et reprend sont exécution 10ns plus tard.
La notation D <= #10 Q; signifie que l'affectation est prévue pour dans 10ns. L'affectation est non bloquante, le processus n'est pas stoppé.

 

Question 1

Parmi ces trois processus il en est deux qui relèvent de la seule modélisation, alors que le troisième peut à priori indifféremment être destiné à la modélisation ou à la synthèse, quel est-il ?

 

Question 2

Donner un chronogrammes précis d'évolution des signaux H, D et Q en fonction du temps physique + temps symbolique.
A quelle date (physique + symbolique) Q passe-t-il pour la première fois à 1 ?

Exercice 2

Soit le dispositif représenté ci-dessous. C'est un registre à décalage à trois étages. A chaque front d'horloge, le contenu d'un registre est tranféré dans le suivant.

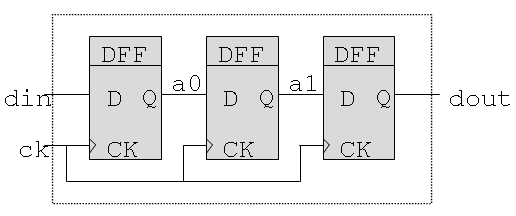
Registre à décalage à 3 étages

 

Question 1

Parmi les quatre descriptions Verilog ci-dessous, laquelle(s) est (sont) correcte(s), et pourquoi ?

module REGS(CK, DIN, DOUT); input CK, DIN; output DOUT; reg DOUT; reg A0, A1; always @(posedge CK) begin   A0 = DIN;   A1 = A0;   DOUT = A1; end endmodule	module REGS(CK, DIN, DOUT); input CK, DIN; output DOUT; reg DOUT; reg A0, A1; always @(posedge CK) begin   A0 <= DIN;   A1 <= A0;   DOUT <= A1; end endmodule	module REGS(CK, DIN, DOUT); input CK, DIN; output DOUT; reg DOUT; reg A0, A1; always @(posedge CK)   DOUT <= A1; always @(posedge CK)   A1 <= A0; always @(posedge CK)   A0 <= DIN; endmodule	module REGS(CK, DIN, DOUT); input CK, DIN; output DOUT; reg DOUT; reg A0, A1; always @(posedge CK)   DOUT = A1; always @(posedge CK)   A1 = A0; always @(posedge CK)   A0 = DIN; endmodule
Version 1	Version 2	Version 3	Version 4

La notation D <= Q; signifie que l'affectation est non bloquante : différée à la fin du delta-cycle courant
La notation D = Q; signifie que l'affectation est bloquante : elle est exécuté instantanément
La notation always @(posedge CK) signifie que le processus est sensible à un front montant de CK : il n'est réveillé et exécuté que sur front montant de CK.